Mega-wut? Making sense of energy metrics (part 2)

This is part 2 of our series on making sense of energy metrics. If you missed part 1, read it first here.
1. So how much energy do we use?
The average American household uses about 30 kilowatt-hours over the course of a day. If we only had 30 states, I’d have a great mnemonic device for remembering that.
Unsurprisingly, 30 kWh a day is way more energy than the rest of the world uses, to say nothing of the half-a-billion people in sub-Saharan Africa who have no access to electricity at all.
The majority of Americans' energy consumption goes towards heating and cooling our large, poorly insulated, single-family homes.
(Heating and cooling accounts for 44% of the total energy used by residential buildings in the U.S. and contributes 20% of our overall greenhouse gas emissions. Implementing more energy efficient ways to heat and cool our buildings, like heat pumps, is a big part of the clean energy transition.)
We’re trying to contextualize all these big numbers here, right? So let’s solve a word problem.
2. How many homes can a nuclear reactor power?
If a nuclear reactor produces a constant 1 Godzilla gigawatt, and the average American family uses 30 kilowatt-hours a day, how many homes can one nuclear reactor power?
First, let's convert the reactor's power capacity to our daily energy requirements:
1 GW = 1,000 MW = 1,000,000 kW
1,000,000 kW × 24 hours = 24,000,000 kWh per day
Now, let's calculate how many homes 24 million kWh per day can supply:
Total daily energy output ÷ Energy consumption per home = Number of homes
24,000,000 kWh per day ÷ 30 kWh per day = 800,000 homes
So, a 1 GW nuclear reactor can supply about 800,000 American homes with all the energy they need.
...right?
Wrong!! In reality, a 1 GW nuclear reactor can only supply 700,000–750,000 homes with energy. That’s because…
3. When electricity travels over power lines, some of it escapes as heat
This is an important concept with many ramifications: some energy always freaking escapes as heat whenever you move or transform it.
In the U.S., our shitty 40-year-old power lines (which have a 50-year lifespan, FYI) lose 5–10% of their electric load during ‘transmission’, i.e. when electricity gets sent from wherever it’s generated to wherever it’s going. The term for this is 'heat loss'.
5–10% might not seem that significant, but in this scenario it represents up to 100,000 homes that will need to get their energy elsewhere.
Engineers have devised ways to minimize heat loss. One is to use high-voltage power lines to send electricity across long distances. The farther electricity travels, the more heat loss it experiences—but a higher voltage reduces heat loss.
Fun fact: China, which is whooping the rest of the world’s ass in the renewable energy game, has constructed Ultra-High-Voltage (UHV) transmission lines to connect their giant northern and southern energy grids with minimal heat loss. Unfortunately, we Americans are too corrupt and short-sighted to build UHV lines of our own. How sad.
But wait, what does voltage have to do with heat loss? And what the eff is voltage, anyway?
4. What is voltage?
Voltage is defined as the difference in electric potential energy between two points.
Yeah...
Rather than explain what that means myself (I’d be too good at it), I’ve asked Dr. Aarati, Green Juice illustrator-extraordinaire and actual PhD, to once again do the hard part for me.
Here’s what she came up with:
"Imagine there’s a large tank of water sitting on the edge of a cliff. While the water is safely in the tank, it can’t do any work. It’s not moving, it has no energy. So its potential to do work (i.e. its ‘potential energy’) is zero.
Now imagine we tip the tank over the cliff. The water pours out and falls towards the ground below. As it falls, the water suddenly has movement and energy and the potential to do work. How much potential? That depends on how high the cliff is.
Voltage = the height of the water tank
This is essentially how voltage works. Voltage is the difference in electrical potential energy between two points. In this example, the two points would be the top of the cliff and the ground. The higher the voltage (i.e. the higher the cliff), the more potential there is to do work.
But we don’t just want to pour our water onto the ground! We want to put that water to good use. So let’s attach a garden hose to our water tank and direct the water’s flow.
Now, you’ve probably never thought about the diameter of your garden hose before. But the diameter of the hose matters: it affects how much water can flow through the hose per second. A hose with a large diameter will allow more water molecules to flow, whereas a smaller diameter will allow less water to flow. We call that rate of flow the current.
Current = the amount of water flowing through the hose per second
Water current is the same thing as electrical current, except instead of water molecules, we’re talking about the flow of electrons. And like electrons, which always move at just under the speed of light, the water going through the hose is moving at the speed of gravity… no faster, no slower. (Okay, it’s not a perfect comparison because gravitational acceleration is not a constant speed, but just go with it!)
If we were to raise the height of the tank, the hose would stretch and become thinner, which means less water can flow through it per second.
The opposite is also true: if we lowered the height of the tank, the hose would relax and its diameter would increase, allowing more water to flow.
From this we can extrapolate: when we increase voltage, we decrease current, and when we decrease voltage, we increase current."

Thank you, Dr. Aarati!
But we still don't know why a high voltage with a low current leads to less heat loss as electricity travels over power lines.
5. Why does high voltage and low current reduce heat loss?
The answer: it’s all about the current.
Think about water molecules traveling through the garden hose. As the molecules rub against the hose walls and each other, they create friction, and friction generates heat. If you read our post about induction stoves, you’ll remember that electricity functions in a similar way: ‘electromagnetic friction’ is created when electricity encounters natural resistance in whatever object it’s traveling through. And there just so happens to be natural resistance in power lines.
So, the higher the current, i.e. the thicker the garden hose, the more molecules you can push through it, the more heat it generates. Conversely, the thinner the hose, the smaller the volume of molecules you can push through and the less heat it generates. Thus, to minimize heat loss, we want a low current so there's less friction.
Two relevant laws of physics explain the relationship between voltage, current, and resistance—Ohm’s Law and Joule’s Law—but Jon is concerned people will stop reading if we write out any more formulas, so you can look those up on your own.
6. Do we adjust the voltage and current for other reasons?
Indeed we do! A critical component of our power grid is the ‘transformer’, a device we use to 'step up' or 'step down' electric voltage (and therefore decrease or increase current).
When we use high-voltage power lines to transmit electricity, that electricity does not go directly to your living room. If it did, your house would explode.
Instead, the electricity makes a pit stop at a nearby 'substation', where a transformer steps down the voltage to something our homes can handle. It then gets distributed as needed to homes and businesses on lower voltage power lines, which are sometimes buried.
We adjust voltage and current for a variety of reasons:
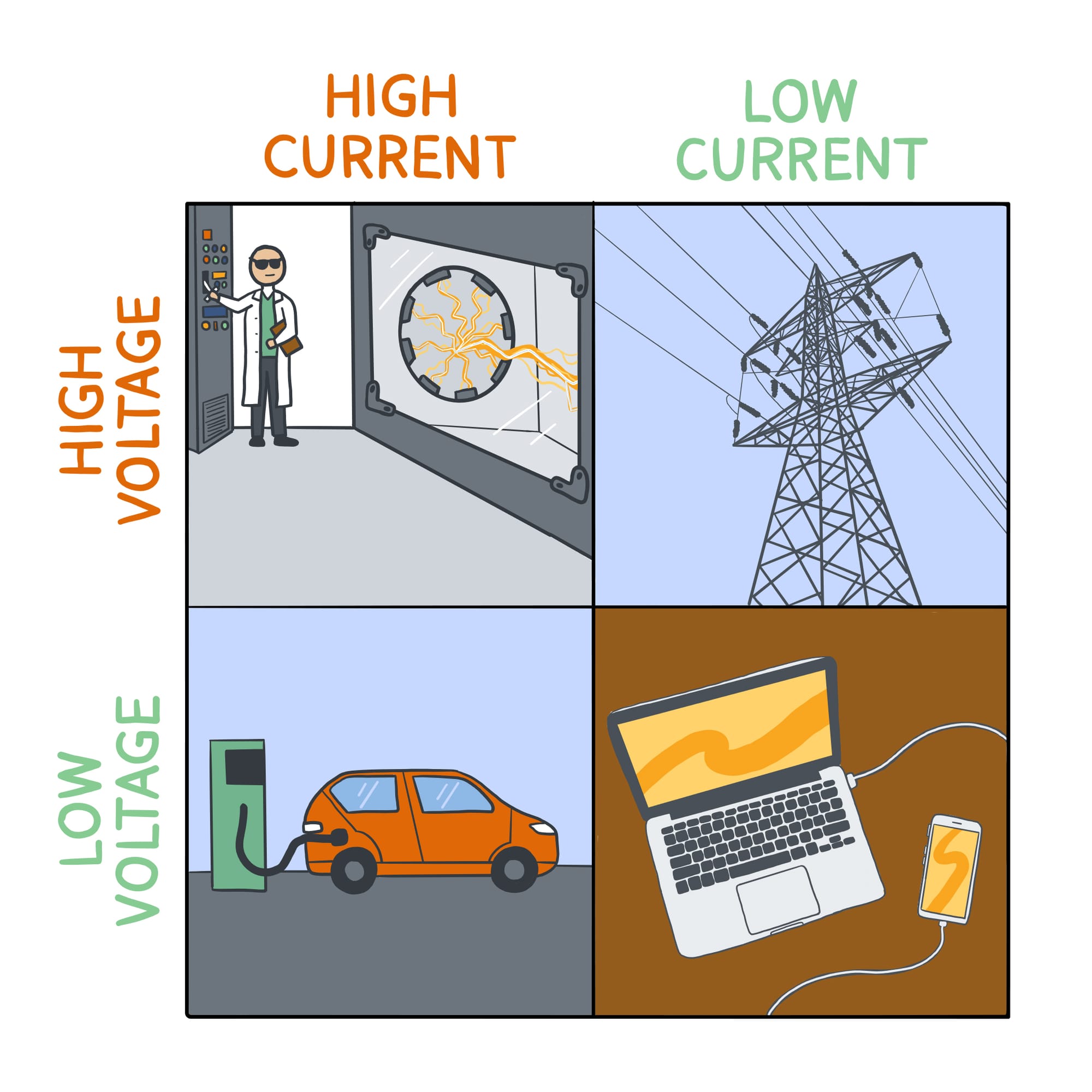
High voltage x high current = high power
Are you an energy physicist working in a lab somewhere like at NREL? If not, you don’t need this. Do NOT touch.
High voltage x low current = medium power
High voltage and low current minimizes the energy lost through heat. Perfect for sending electricity long distances over power lines.
Low voltage x high current = medium power
If you are charging an electric car, using large appliances or computers, or spot welding for some reason, then low voltage with a high current is best.
Low voltage x low current = low power
Good for small electric devices like phones, laptops, and other small electronics that you want to power without blowing up.
Does your brain hurt yet? That means it's working! There's just one more post in this series.




Member discussion